issie's whisper
2018年12月23日日曜日
鶏口牛後
当塾の父母面談が終わり、学校の3者面談もそろそろ終わる頃です。中3生にとっては進路決定する重要な面談となっているわけですが、保護者様と色々お話させていただく中で、勿論志望校決定の最大の要素が偏差値であることはゆるぎないところではあります。但し「鶏口となるも牛後となるなかれ」という言葉にあるように、「大きな集団で人のしりについているよりも、小さな仲間でも、その頭となったほうがよい」といった趣旨で使われますが、この言葉を高校受験で用いると、「偏差値の高いチャレンジ校にギリギリで合格しても、その学校の授業についていけなくなるだけ、それよりは相応校に入って、そこでトップを目指す方が得策である」といった意味合いになると思います。僕は相応校でもそこでトップクラスにいるために日々の鍛錬を継続することは、大学受験に挑む「勉強での体力」を自然に鍛えることにつながると思っていますので、いつも父母面談ではこのお話をさせていただいています。但し、あと一歩の頑張りでチャレンジから相応校へと偏差値が上がる余地が見えている場合、例えば理科社会の知識面が補充することができれば、全体偏差値が向上するような場合、そこで生徒が「どうしてもチャレンジしてあの学校に入りたい!」と強く心に決めている場合は、例え、もし合格して入学する際の順位で上位まで食い込むことができなくてもあえてチャレンジするべきだと思っています。勿論、安全校を確保してのチャレンジということにはなりますが…。生徒の「どうしても入りたい」という強い意欲がこの時期からは結果に大きく影響すると思います。最後までその強い意志を持ったまま頑張っていきましょう!
2018年9月27日木曜日
rego
年長の息子がレゴブロックにハマっていまして、先日は自分で作ったレゴブロックの作品が、動き出し、音を奏でるといった、レゴファンの夢をかなえてくれるレゴの製品『レゴ ブースト』を体験してきました。身体が大きいので小学生と間違われましたが、2020年の小学校でのプログラミング教育の必修化が決まっていることもあり、習い事の一つとしてどんどん増えてきています。年長にもなると何かしら習い事をされている子供が本当に昔と比べて多くなりましたが、僕自身も時間とお金が許す限りにいろいろさせてみて、本人が嫌ならやめればいいし、楽しいなら続ければいいかなといったように選択させてあげるといった流れを作ってあげたらなと思っています。僕は習い事を系統に分けるとスポーツ系、学習系、芸術系があると思っていますが、それぞれ一つずつが理想かなと考えています。レゴについては知育に効果的と言われ、発想力や想像力、構築力、問題解決力などを遊びながら身に付けられると言われていますが、幸いにも息子は年少あたりで興味を持ち始めてくれたこともあり、今回是非プログラミングについては早い段階から興味をもってくれたらと思って体験させていただきました。ロボットとipadをBluetooth接続し、命令を送るのですが、子どもたち(息子も含め)はipadを使用することも、『Bluetooth』や『プログラミング』といった言葉にも特に抵抗もなく、リテラシーの高さを感じました。息子が体験したのは目的地までロボットを動かすというミッションだったわけですが、難なくクリア。本当に未恐ろしいですね。僕が子どもの頃はこんな素晴らしい教材は存在していなかったので、本当に今の子供たちがうらやましい限りです。算数には答えがありますが、「プログラム」には正解のない課題が多く与えられるので、自由な発想で自由にクリエイティブにできるのがいいですよね。どんな回答も間違っていないという部分が僕はとても好きです。
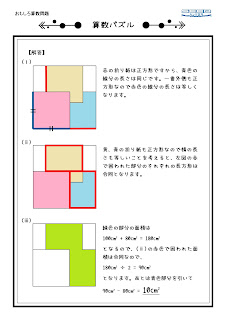
2018年6月21日木曜日
塗り重ねていくこと
※今回の算数パズルでは折り紙を重ねてみました(笑)
2018年6月6日水曜日
補助線ってどうやって引くの??
先日ある図形の問題を解いていた生徒に「先生!ヒント頂戴!!」と言われたので「補助線を引いてごらん」とお答えしましたところ、「補助線って適当に引くの?」と…。「おいおい、もうちょっと考えようよ。」算数や数学の図形問題では、補助線をどこに引くかで問題が解けたり、解けなかったりします。僕は図形問題が苦手な理由の一つに、補助線を引かなければならないからだと思っています。パターン暗記に頼っている生徒の多くは今回のケースのように「とりあえずこことここを結んで…」と適当に補助線を引き、その後「あれ?結局何をすればいいんだろ?」とフリーズしてしまいます。「補助線」とはその名の通り「その線によって助けられる」というものではなくてはなりません。「ここに線を引けば合同形ができる。」「ここに線を引けば、この部分の角度が求められる。」「ここに線を引けば、この図形の面積が求められる。」など、その線によって有力情報がうまれるかどうかが大事なのですね。また、最終的に何を求めたいかによっても、最適な補助線の引き方が変わってくると思います。聞かれているものによって、補助線の引き方が変わってくるというのもぜひ身に付けてほしいと思います。「必要な情報を求めるために補助線を引く」という視点を大切にしながら図形問題を解くように心がけてみましょう。もしかしたら、「分からない問題を考えることを楽しむ」ということが、補助線を引くコツなのかもしれませんね。(今回の写真の問題では一見難しそうな問題ですが、補助線によって合同な正三角形を作ることができれば、小学低学年でも簡単に求められます。まさか"√"なんて使いませんよ笑)


2018年5月24日木曜日
破壊と分解
これは何の道具かわかりますか?皆さんのファイルノートにはさんでいるプリントに穴開ける道具でルーズリーフパンチ「グリッサー」と呼ばれる文房具です。当塾で10年以上も使用しているものですが、先日僕が使用しているときにスライダーの部分が中で外れてしてしまいました。このままでは使い物にならない状態なので、とりあえず「分解」して直そうと試みることに…。注意していただきたいのが、「破壊」と「分解」はモノをバラバラにするという意味では同じですが、「破壊」は元の形がわからなくなります。一方「分解」は一つ一つの部品に分け、部品の意味を理解する。そしてもう一度組み立てることもできます。今回の僕の場合は「破壊」ではなく「分解」です笑。この「グリッサー」ですが連続ロット刃を波状に押し下げて軽い力で一気に穴をあける仕組みなのですが、こうやって分解してみないと気付かないことってたくさんあります。しかし、実際には身近なものといってもその多くがブラックボックス化されており、簡単に分解できないものや分解できても複雑すぎて仕組みが分からないものが多いですね。その為、「分解=壊すこと-してはいけない。モノは使えることができればよく、仕組みを理解する必要はない」と考えてしまう子供たちが多いと思います。是非、中を開けて不思議に思う意識や中を開けてみたいという好奇心を持ってもらえたらと思います。さて、今回スライダーの部分が中で外れていたのは中に蓄積されたゴミが原因でつっかかりが生まれ、固くなっていたからですが、ゴミを取り除き、CRC(潤滑油)をさして組み立てるとまた購入時のときのように滑らかに穴をあけることができるようになりました。この例のように勉強を頑張っているのに成績が上がらないは必ず原因があるはずです。このまま成績が上がらないと思っていませんか。そういうときは「分解」してみることをお勧めします。数学で例えるなら分数計算ができますか?通分は?約分は?以前書きましたができるだけ細かい要素に「分解」すれば意外と簡単に自分が躓いている部分(原因)が見えてくるはずです。来週から生徒と講師の個人面談が始まります。僕たちシードゼミスタッフは潤滑油になりますので、是非悩みを打ち明けてみてください。
2018年5月23日水曜日
苦手科目を克服したある生徒の話
高校生は定期テスト真っ最中です。そんな中「数学いやや。」「単語覚えられへん。」と定期テストが始まっているにも関わらず苦手科目に悩ました生徒たちが口々に言います。どうすれば苦手と思わなくなるのでしょうか。それは簡単なことで、その科目でよい点をとることです。「とれないから苦手科目や!」と言われそうですが…。ある生徒の話です。彼女は中3の途中から通い始めて数学がとても苦手でした。真面目に通ってくれていたので数学の成績はなんとか「3」だったのですが、小学校の内容でもある分数計算や小数計算などの知識もなく、毎回居残り補習といった状態でした。その後、なんとか無事公立高校に合格し、高校生になって今も通い続けてくれています。勿論数学が苦手なので、数学だけを個別授業で受講してくれているわけですが、なんと、高校2年生のときに学年トップ。成績は「5」をとれるようになりました。しばらくは数学への苦手意識はすぐには治りませんでしたが、その後何度もトップをとるうちに数学は「得意科目」へ。今では「苦手」という言葉は全く聞かなくなりました。時間はかかりましたが、彼女が克服できた理由は、「真面目にコツコツ勉強を継続したこと」「苦手だからといってその科目から逃げなかったこと」です。さらに言えば「苦手だから勉強しよう」と思ったことが最大の要因だったのではないでしょうか。今彼女は自分の進路実現に向け本当に努力しています。人はよい結果が出ればさら頑張れます。その喜びを得るためにみんな努力しています。だからみなさんも今結果が出なくても焦ることはありません。見えない部分の成長が、見える部分に変えていきます。地道に努力を続けて、しっかり基盤になったときはじめて本物の結果(実力)が手に入ります。ですから、結果が必ず出てくると信じて頑張りましょう!
2018年5月21日月曜日
ノートは要点をおさえてまとめよう!
高校生の定期テストも今週ということで中学生・高校生ともに自習教室を積極的に利用いただき、まるで入試直前かのような緊張感ある雰囲気になっています。僕は定期テストの範囲表に記載されている教科書や問題集のページ数を確認するのは勿論のこと、生徒たちの学校の授業ノートを学校、学年、クラスごとに必ず目を通すようにしています。そこで真面目な生徒さんに多いのが不必要な書き込みが多いことです。ある生徒さんは授業中での先生の話や参考書の内容を書けるだけ書いて、一見綺麗には書かれているのですが、一番重要な部分がよくわからない状態でした。ある有名なイラストレーター和田誠さんの似顔絵のお話ですが、彼が描く似顔絵はシンプルですが、一目で誰か分かるように描かれています。これはその人の顔の特徴の中でも、一番重要なところを、的確にとらえているからです。目的とするものを表現するために、絶対に必要な部分と、省いても良い部分を見分ける力がひときわ優れているのだと思います。この「要点をとらえる」ことは勉強にもとても大切です。テストにおいても、重要な部分を抜き出したり、要点をまとめる問題に出くわしたりします。そんなときに素早く物事の要点がとらえる力が備わっていたら、普段の勉強もテストの点数も、ワンランクアップできるはずですね。要点がとらえることができればスピードも上がります。但し、たくさんの情報の中で、重要なところを過不足なく取り出して整理していく能力は簡単に身につくものではありません。沢山の量をこなすことで鍛えられ、徐々に身に付けていくものです。和田誠さんも絵が好きで人の顔を描くのが楽しくで、たくさん描いたからこそ、要点を見抜く力が養われ、シンプルなのに味のある似顔絵を描けるのだと思います。勉強でも様々な問題、量をこなした分だけ、要点をしっかりとらえるようになり、いつでも自然に発揮できる力になっていくと思っています。そしてその力が勉強の質を確かにアップさせていく武器となっていくはずです。
登録:
投稿 (Atom)
鶏口牛後
当塾の父母面談が終わり、学校の3者面談もそろそろ終わる頃です。中3生にとっては進路決定する重要な面談となっているわけですが、保護者様と色々お話させていただく中で、勿論志望校決定の最大の要素が偏差値であることはゆるぎないところではあります。但し「鶏口となるも牛後となるなかれ」という...
-
issie’s読書感想文。またもや山田詠美さんです。作品は「蝶々の纏足・風葬の教室」。今回は「蝶々の纏足」の感想を書いてみます。幼なじみのえり子に支配され、いつも引き立て役の瞳美の女の子二人の物語。このえり子の支配の仕方が支配していると誰にも気付かせないような巧妙さなのですが、か...
-
各中学、そしてほとんどの高校が新学年としての初めての定期テストを終了しました。結果もぼちぼち出て、報告してくれていますが、結果を見てみると勉強というのは本当に正直だなぁと思います。特に定期テストでは範囲も指定されていますし、その範囲も模試や入試ほど広くありません。日々の学習がどれ...
-
先月より肉体改造を目的に大きいからだをさらに大きくしようとジムに通い始めました。…嘘ですw。運動不足解消とダイエットが目的です。ダイエットに筋トレ?と思うかもしれませんが、ダイエットのために筋トレをするというのは理にかなっています。筋肉量がアップすると基礎代謝量が上がるからですね...